Probabilités définitions et explications

Probabilités : définitions et explications

A) Expérience aléatoire

Le calcul des probabilités sert à chiffrer la possibilité d’un événement aléatoire.

Définition

Un événement aléatoire est un événement dont le résultat dépend complètement du hasard.

Cela signifie qu’on ne peut pas influencer un événement aléatoire, sinon, ce n’est plus un événement aléatoire.

Par exemple, on a beau souffler sur des dés, réciter des incantations, on n’arrivera pas à influencer le résultat du dé. Quant aux billets de loterie, choisir des nombres signifiants pour vous (comme la date de naissance de votre mère ou le nombre de démérites que vous avez accumulés) ne vous fera pas plus gagner le gros lot que des nombres choisis au hasard.

Exercice : indiquez si l’expérience est aléatoire ou non.

Calculer le temps pris par la grande aiguille d’une horloge pour faire un tour complet.

Lancer une pièce de monnaie dont les deux faces sont identiques.

Observer le nombre d’heures d’ensoleillement au cours d’une journée.

Tirer une carte dans un jeu de 52 cartes à jouer.

Compter le nombre de pattes d’un éléphant.

Gagner une partie de tic-tac-toe.

Être hospitalisé d’ici un an si l’on est actuellement en bonne santé.

B) Expérience aléatoire simple ou composée

Définition
Une expérience aléatoire qui se déroule en une seule étape est dite simple.

Si on fait suivre plusieurs expériences aléatoires simples, on se retrouve donc avec plusieurs étapes.

Définition
Une expérience aléatoire qui se déroule en plusieurs étapes est dite composée.

Un exemple d’expérience composée serait d’acheter un billet de 6/49 et un autre de Super 7. Il s’agit de 2 tirages séparés. Si vous achetez l’Extra en achetant un billet de Super 7, vous avez encore une expérience composée, car l’Extra n’est ni plus ni moins qu’une autre loterie.

Exercice : dites si les expériences suivantes sont simples ou composées.

Lancer une pièce de monnaie une seule fois.

Tirer au hasard une des lettres du mot «hiver».

Piger deux lettres dans un jeu de Scrabble.

Lancer 3 pièces de monnaie.

Former une combinaison de 3 chiffres sur un cadenas.

Obtenir une consonne en tirant au hasard une lettre du mot «société».

Tirer deux noms d’un chapeau contenant tous les noms des élèves d’une classe.

C) Probabilité d’un résultat dans une expérience aléatoire simple
Grosso modo, une probabilité est une comparaison, tout comme une fraction, un rapport ou un pourcentage. On compare le nombre de cas probables (le résultat qu’on veut voir arriver) sur le nombre total de cas possibles (l’ensemble des résultats qui pourraient arriver).

Par exemple, la probabilité qu’un dé donne le résultat «6» est :

P(6) =
1 cas probable = 1/6

6 cas possibles

Exercice : quelle est la probabilité...

de tirer la lettre «g» dans le mot «Gargouille»?

de tirer une bille rose parmi 5 billes roses et 7 billes bleues?

de tirer un roi dans un jeu de cartes?

de tirer un chiffre pair dans une urne contenant des jetons numérotés de 0 à 9?

de tirer un chiffre supérieur à 7 dans la même urne?

de tirer un multiple de 3 dans cette urne?

D) Expérience aléatoire composée : nombre de résultats

Définition
On appelle l’ensemble des résultats possibles «univers des possibles» et on le symbolise par la lettre grecque Ω (lire «oméga»).

Dans le cas des résultats du dé, l’ensemble Ω = {1, 2, 3, 4, 5, 6}. Ce sont les seuls résultats possibles lorsqu’on lance un dé.

Par contre, si l’on lance deux dés, on a plus de résultats possibles : les résultats possibles du premier sont {1, 2, 3, 4, 5, 6}, ainsi que pour le deuxième.

Il y a plusieurs façons de montrer les résultats combinés d’une expérience aléatoire composée.

1. une grille de résultats

Reprenons le dernier exemple avec les deux dés (où, par exemple, le couple (1,5) signifie que le premier dé a donné le résultat «1» et le deuxième, le résultat «5»)

	1	2	3	4	5	6
1	(1,1)	(1,2)	(1,3)	(1,4)	(1,5)	(1,6)
2	(2,1)	(2,2)	(2,3)	(2,4)	(2,5)	(2,6)
3	(3,1)	(3,2)	(3,3)	(3,4)	(3,5)	(3,6)
4	(4,1)	(4,2)	(4,3)	(4,4)	(4,5)	(4,6)
5	(5,1)	(5,2)	(5,3)	(5,4)	(5,5)	(5,6)
6	(6,1)	(6,2)	(6,3)	(6,4)	(6,5)	(6,6)

Les résultats possibles sont donc Ω = {(1,1), (1,2) , (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}, ce qui se chiffre à 36 résultats possibles.

2. un diagramme de Venn

Soit l’expérience qui consiste à prendre aléatoirement une boule de couleur rouge ou verte (possibilités {R,V}), et le résultat d’un dé (possibilités {1, 2, 3, 4, 5, 6}). En menant toutes les flèches possibles du premier résultat au deuxième, on peut dénombrer et nommer tous les résultats combinés possibles.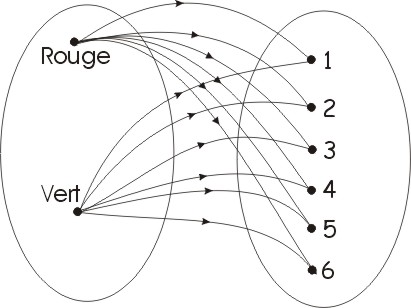

Les résultats possibles sont donc Ω = {(R,1), (R,2), (R,3), (R,4), (R,5), (R,6), (V,1), (V,2), (V,3), (V,4), (V,5), (V,6)}, ce qui se chiffre à 12 résultats possibles.

3. un arbre

Quand il y a plus de deux expériences aléatoires, l’arbre est le meilleur outil.

Imaginons un jeu de cadavres exquis, où chaque participant doit dessiner une tête sur une feuille de papier, plier la feuille afin de cacher son dessin et la faire passer au voisin afin que celui-ci dessine un corps, et ainsi de suite jusqu’à ce qu’on déplie la feuille et qu’on voie un dessin cocasse représentant une tête de pirate sur un corps de ballerine avec des pattes d’autruche!

Supposons donc qu’on ait le choix de dessiner un pirate, un joueur de hockey et une chanteuse populaire à la Christina Aguilera. Voici l’arbre des possibilités:

Les résultats possibles sont donc Ω = {(tête de pirate, corps de pirate, jambes de pirate), (tête de pirate, corps de pirate, jambes de hockeyeur),etc...}, ce qui se chiffre à 27 résultats possibles.

	Exercice : donnez le nombre de résultats possibles dans les expériences aléatoires suivantes. Le nombre de menus différents si la cafétéria offre 2 choix de soupes, 3 choix de plats principaux et 4 choix de desserts. Le nombre de combinaisons possibles au 6/49. Le nombre de combinaisons si on choisit une saison de l’année et un chiffre entre 1 et 5 (inclusivement). Trois villes, A,B,C, sont reliées par des routes. Cinq routes relient A et B, quatre routes relient B et C et trois routes relient A et C. Combien de trajets possibles? Le nombre d’ensembles si Diana possède 2 pantalons (un rose et un jean), 3 chandails (un vert, un blanc et un noir) et 2 chemisiers (un rose et un rouge). Former une phrase avec un nom (Danielle, Maya, Stéphanie), un verbe (manger, prendre, briser) et un complément direct (pomme, coeur, fleur). On veut choisir deux solistes dans une chorale de 8 chanteurs.

F) Probabilité d’un résultat dans une expérience aléatoire à plusieurs étapes

Définition

Des événements qui ont la même chance de se produire sont dits équiprobables

Lorsque des événements sont équiprobables, on n’a qu’à répartir les probabilités entre les différents résultats possibles.

Problème :

Dans une école, les groupes d’élèves de deuxième secondaire sont formés de façon aléatoire. Il y a 4 enseignants de français et 4 de mathématique. Chacun enseigne à 4 groupes d’élèves. Quelle est la probabilité que Sandra et son amie aient toutes les deux les mêmes enseignants en français et en mathématique?

Il y a 16 couples d’enseignants possibles. Sandra et son amie ont donc 1 chance sur 16 d’avoir les mêmes enseignants. La probabilité est donc

P(avoir les mêmes enseignants) = 1/16.

On remarque que P(avoir le même enseignant en français) =1/4 et P(avoir le même enseignant en maths) =1/4.

On constate donc qu’on peut multiplier 2 probabilités d’événements indépendants pour obtenir la probabilité de ces 2 événements combinés :

P(avoir les mêmes enseignants)

= P(le même enseignant de français) • P(le même enseignant de maths)

= ¼ • ¼

= 1/16